how to draw a phase portrait

Testify Mobile Observe Evidence All NotesHide All Notes

Mobile Discover

You lot appear to be on a device with a "narrow" screen width (i.e. yous are probably on a mobile phone). Due to the nature of the mathematics on this site it is best views in landscape mode. If your device is non in landscape style many of the equations volition run off the side of your device (should be able to coil to run across them) and some of the menu items volition be cut off due to the narrow screen width.

Section 5-half dozen : Phase Airplane

Before proceeding with actually solving systems of differential equations there's one topic that nosotros demand to take a look at. This is a topic that's not ever taught in a differential equations class but in case you're in a course where it is taught we should embrace it so that y'all are prepared for it.

Let's showtime with a general homogeneous system,

\[\begin{equation}\vec ten' = A\vec 10\label{eq:eq1}\end{equation}\]

Observe that

\[\vec x = \vec 0\]

is a solution to the system of differential equations. What we'd like to ask is, do the other solutions to the system arroyo this solution as \(t\) increases or practice they move away from this solution? We did something similar to this when we classified equilibrium solutions in a previous section. In fact, what we're doing hither is merely an extension of this thought to systems of differential equations.

The solution \(\vec ten = \vec 0\) is called an equilibrium solution for the system. Every bit with the unmarried differential equations instance, equilibrium solutions are those solutions for which

\[A\vec x = \vec 0\]

We are going to presume that \(A\) is a nonsingular matrix and hence will have only one solution,

\[\vec x = \vec 0\]

and and so we will have only 1 equilibrium solution.

Dorsum in the single differential equation case recall that we started by choosing values of \(y\) and plugging these into the part \(f(y)\) to determine values of \(y'\). We then used these values to sketch tangents to the solution at that item value of \(y\). From this we could sketch in some solutions and use this information to classify the equilibrium solutions.

We are going to do something similar here, but it will be slightly different also. First, we are going to restrict ourselves down to the \(2 \times ii\) case. So, we'll be looking at systems of the form,

\[\begin{array}{*{20}{c}}\begin{align*}{{x'}_1} & = a{x_1} + b{x_2}\\ {{x'}_2} & = c{x_1} + d{x_2}\end{align*}&{\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}\vec 10' = \left( {\begin{array}{*{20}{c}}a&b\\c&d\terminate{array}} \right)\vec x}\end{array}\]

Solutions to this system volition be of the grade,

\[\vec x = \left( {\begin{assortment}{*{20}{c}}{{x_1}\left( t \right)}\\{{x_2}\left( t \right)}\finish{array}} \right)\]

and our single equilibrium solution will be,

\[\vec x = \left( {\begin{array}{*{20}{c}}0\\0\end{array}} \right)\]

In the unmarried differential equation case we were able to sketch the solution, \(y(t)\) in the y-t plane and see bodily solutions. However, this would somewhat hard in this case since our solutions are actually vectors. What we're going to exercise here is think of the solutions to the system as points in the \({x_1}\,{x_2}\) plane and plot these points. Our equilibrium solution will correspond to the origin of \({x_1}\,{x_2}\). plane and the \({x_1}\,{x_2}\) plane is called the phase plane.

To sketch a solution in the phase airplane we can choice values of \(t\) and plug these into the solution. This gives us a signal in the \({x_1}\,{x_2}\) or stage plane that we tin can plot. Doing this for many values of \(t\) will and then requite us a sketch of what the solution will be doing in the phase aeroplane. A sketch of a particular solution in the phase plane is chosen the trajectory of the solution. One time nosotros have the trajectory of a solution sketched we can then enquire whether or not the solution will arroyo the equilibrium solution as \(t\) increases.

We would like to be able to sketch trajectories without actually having solutions in hand. There are a couple of means to do this. We'll look at ane of those here and we'll look at the other in the side by side couple of sections.

1 manner to go a sketch of trajectories is to practise something similar to what we did the outset time we looked at equilibrium solutions. We can cull values of \(\vec ten\) (annotation that these will be points in the phase plane) and compute \(A\vec x\). This will requite a vector that represents \(\vec 10'\)at that particular solution. Equally with the single differential equation example this vector will be tangent to the trajectory at that bespeak. Nosotros can sketch a bunch of the tangent vectors and and then sketch in the trajectories.

This is a fairly piece of work intensive way of doing these and isn't the way to do them in general. Notwithstanding, it is a way to get trajectories without doing any solution piece of work. All we need is the system of differential equations. Let's have a quick look at an example.

Example 1 Sketch some trajectories for the system, \[\begin{array}{*{20}{c}}\begin{align*}{{ten'}_1} & = {x_1} + 2{x_2}\\ {{10'}_2} & = iii{x_1} + two{x_2}\end{marshal*}&{\hspace{0.25in} \Rightarrow \hspace{0.25in}\vec 10' = \left( {\brainstorm{array}{*{xx}{c}}1&2\\three&ii\end{array}} \right)\vec ten}\end{array}\]

Prove Solution

So, what we need to do is choice some points in the phase plane, plug them into the right side of the system. We'll practise this for a couple of points.

\[\begin{align*}\vec x & = \left( {\begin{array}{*{20}{c}}{ - 1}\\1\end{array}} \right) & \Rightarrow \hspace{0.25in}\vec x'& = \left( {\begin{array}{*{20}{c}}1&ii\\three&2\finish{array}} \right)\left( {\begin{array}{*{20}{c}}{ - 1}\\ane\stop{assortment}} \correct) = \left( {\begin{array}{*{xx}{c}}ane\\{ - 1}\end{assortment}} \correct)\\ \vec x & = \left( {\begin{array}{*{20}{c}}2\\0\end{array}} \correct) & \Rightarrow \hspace{0.25in}\vec ten' & = \left( {\begin{array}{*{20}{c}}1&2\\3&two\finish{array}} \right)\left( {\begin{assortment}{*{xx}{c}}ii\\0\finish{array}} \right) = \left( {\brainstorm{array}{*{20}{c}}2\\6\terminate{array}} \right)\hspace{0.25in}\\ \vec x & = \left( {\begin{array}{*{20}{c}}{ - 3}\\{ - two}\terminate{assortment}} \right) & \Rightarrow \hspace{0.25in}\vec ten' & = \left( {\begin{assortment}{*{xx}{c}}1&2\\three&2\cease{array}} \right)\left( {\begin{array}{*{20}{c}}{ - 3}\\{ - 2}\stop{array}} \correct) = \left( {\begin{assortment}{*{20}{c}}{ - seven}\\{ - thirteen}\terminate{array}} \right)\hspace{0.25in}\finish{marshal*}\]

So, what does this tell us? Well at the point \(\left( { - 1,1} \correct)\) in the phase aeroplane there will exist a vector pointing in the direction \(\left\langle {one, - ane} \right\rangle \). At the point \(\left( {2,0} \right)\) there volition be a vector pointing in the direction \(\left\langle {2,half-dozen} \correct\rangle \). At the point \(\left( { - 3, - two} \right)\) there volition be a vector pointing in the direction \(\left\langle { - seven, - 13} \right\rangle \).

Doing this for a big number of points in the phase plane will give the following sketch of vectors.

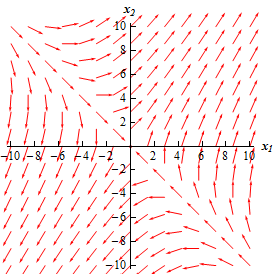
Now all we demand to exercise is sketch in some trajectories. To practise this all we need to do is remember that the vectors in the sketch to a higher place are tangent to the trajectories. Also, the direction of the vectors give the management of the trajectory as \(t\) increases and so nosotros can show the time dependence of the solution by adding in arrows to the trajectories.

Doing this gives the following sketch.

This sketch is called the phase portrait. Usually phase portraits only include the trajectories of the solutions and not whatsoever vectors. All of our stage portraits grade this betoken on will only include the trajectories.

In this case information technology looks like most of the solutions will start away from the equilibrium solution then as \(t\) starts to increment they movement in towards the equilibrium solution and and then eventually start moving away from the equilibrium solution once more.

There seem to exist four solutions that have slightly different behaviors. It looks like 2 of the solutions will offset at (or near at least) the equilibrium solution and and so movement straight abroad from it while 2 other solutions start away from the equilibrium solution and and then move straight in towards the equilibrium solution.

In these kinds of cases we telephone call the equilibrium point a saddle point and we call the equilibrium point in this case unstable since all but 2 of the solutions are moving away from information technology as \(t\) increases.

As nosotros noted earlier this is not generally the manner that we will sketch trajectories. All we actually need to get the trajectories are the eigenvalues and eigenvectors of the matrix \(A\). Nosotros will encounter how to do this over the adjacent couple of sections as nosotros solve the systems.

Here are a few more than phase portraits and so you can see some more possible examples. We'll actually be generating several of these throughout the course of the next couple of sections.

Not all possible phase portraits take been shown hither. These are here to show you some of the possibilities. Brand certain to discover that several kinds tin can be either asymptotically stable or unstable depending upon the direction of the arrows.

Detect the difference betwixt stable and asymptotically stable. In an asymptotically stable node or screw all the trajectories volition move in towards the equilibrium bespeak every bit t increases, whereas a center (which is always stable) trajectory volition just move around the equilibrium bespeak but never actually motion in towards information technology.

Source: https://tutorial.math.lamar.edu/classes/de/phaseplane.aspx

Posted by: gillenwatersquill.blogspot.com

Share this post